The game of life

An essay on the beauty of complexity, emergence, and life.

---

In memory of John Conway, the British mathematician who is known for development of the Game of Life, and who recently passed away in April 2020 after developing symptoms of COVID-19.

---

Most of us may have played chess, or any other board game based on a small set of few rules. One could cram all the fundamental rules of the game, and yet end up on the losing side. A seasoned chess player is one who has a variety of openings, attacking & defensive moves, and strategies in his repertoire. What sets an expert apart from an unskilled player (who has learned all the basic rules by heart) is his ability to see beyond the fundamental rules as singular prescription to progress the game. The fundamental rules give rise to more intricate and complex states as the game progresses – states which cannot be predicted easily from the basic set of rules. The modern version of the game of chess has been around for about a millennium [1] and we still discover new possibilities in the game that were previously unknown. This is emergence.

A formal definition of emergence is that it can be stated as a phenomenon in which a system comprised of smaller parts displays the properties that cannot be explained by studying its constituents separately. In other words, the ‘whole’ exhibits specific properties which cannot be observed by reducing the ‘whole’ to its constituents. The example of the game of chess clearly explains that. A state of a standard game of chess, say 10 minutes after the start, is quite complex and even though both players have used the same set of fundamental rules to advance the game by each move, the patterns and moments about the center of the chessboard that emerge are novel in their own right. This form of emergence is dubbed as weak emergence – when the properties at the higher level of complexity supervene on the ones present at the lower level. As an example, we can say the complex patterns and moments about the center of a chess board supervene on the basic rules of the game. The significant aspect of weak emergence is that although, in principle, the properties at the higher level can be deduced from the interaction of the entities at the lower level, those properties are unexpected and their deduction is not straightforward. A tiny change in the initial state of the system can yield a catastrophic change in the evolved state later. This makes predictions hard and emergence interesting. Scientific systems exhibit this type of emergence and it does not threaten the tenets of fundamental physics – which to an involved reader, should be obvious from the preceding discussion. On the other hand, strong emergence is radical as it involves the emergent properties at a higher level that do not supervene on the properties of the levels below it. There are hardly any complex, scientific systems which exhibit this form of militant emergence, except maybe the structure of the universe at the most fundamental level.  The examples of emergence and complexity presented in this essay are strictly restricted to the weak version, and emergence and weak emergence will be used synonymously. Strong emergence is a core philosophical topic and I do not want to digress from keeping this discussion within the purview of science.

Emergence is ubiquitous. Our societies supervene on our collective social behavior, which in turn depends on our psychology which is primarily a consequence of our individual minds that emerge from our brains facilitated by our biology, which then further depends on chemistry and so on to molecules and atoms, to electrons, protons and quarks. This reduction can be conceived to go on ad infinitum, or perhaps there may exist a fundamental, non-reducible structure at the core of our reality after all! Whatever that non-divisible stratum is, it must be strongly emergent. 

Democracies, or more precisely emergent democracies are also an example of how a number of political structures, laws and rights come together to create a bottom-up machinery that ensures smooth functioning of a people. Being a bottom-up affair essentially, it is unlikely for a democracy to work when forced top-down – the fact which the leaders of military occupations fail to understand! 

Seeds are a fascinating example of emergence. It is interesting to observe that a single seed (of sunflower) can evolve into a plant that displays, within each flower, a sophisticated pattern of seeds following the Fibonacci sequence. It is not implausible to think that for the complete understanding of properties of a mature organism, and/or how they come about, the dynamics of the gene-specified interactions are equally important as the instructions encoded in the gene itself.    

We can envisage emergence in a different way if we focus our attention to mathematical systems. A famous example is the Conway’s Game of Life (GoL) which is a cellular automaton developed by the British mathematician John Horton Conway in 1970 (and who recently passed away in April 2020 after developing symptoms of COVID-19). The universe of the GoL is an infinite 2D grid of cells, each of which can exist in two states – live (white) or dead (black). Furthermore, each cell has 8 neighbors – right, left, top, bottom and four diagonally adjacent ones. The game is started by any random initial configuration of dead and alive cells and then advanced in time subject to a set of three simple rules [2]:

1. Any live cell with two or three live neighbors survives.
2. Any dead cell with three live neighbors becomes a live cell.
3. All other live cells die in the next generation. Similarly, all other dead cells stay dead.

Advancing a simple initial state with a few alive cells subject to these three simple rules quite clearly reveals how complex patterns can emerge out of simplicity without the involvement of any external aid or intelligence. To illustrate how this happens, I have presented here the animations that I obtained from my own implementation of the Game of Life in MATLAB®. Figure 1 shows a typical ‘Acorn’ structure which comprises of just seven live cells followed by the Video 1 which shows the time evolution of this structure (used as the initial state) in a simulation comprising of about 5000 generations – until the steady state was attained. You might dislike my essays but I bet you will never dislike my choice in music! Video 1 background music is one of my favorites and it makes emergence in GoL all the more alluring and mysterious!!  

Figure 1: The Acorn structure which
comprises of just seven live cells. 
Video 1 on the right shows the time evolution
of this initial state until it reaches stationarity.
Watch in fullscreen mode. [3]

It is quite remarkable that this simple structure ‘Acorn’ blossoms into a whole galaxy of patterns and entities. In addition to the basic ones like squares, some complex patterns are stable like the one which resembles a set of equidistant drop-like entities arranged in a semicircle/circle (or 4 corners of a rhombus), and an oscillating pattern resonating between a ‘+’ shaped symbol and a square region bound by four lines. Furthermore, the most exciting feature of this simulation is the emergence of ‘gliders’ – the translating entities which appear to glide across the whole domain of the game. These gliders act as the messengers in the game and carry information from one part of the universe to the other. Poetic! Beautiful! Mindgasmic!

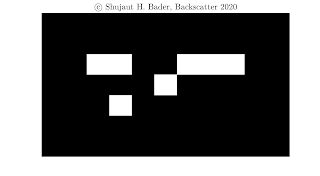
In Figure 2 is shown the ‘Glider Gun’ – a dynamic configuration of a bunch of live cells that can generate these gliders forever. Video 2 shows this gun in action for about 1500 generations. 

Figure 2: The Glider Gun.
Video 2 on the right shows this gun in action,
 generating gliders forever. Watch in fullscreen mode. [4]

Mathematical equations are structures that follow simple rules of logic and algebra. The careful manipulation of these equations may give rise to a different set of mathematical structures/equations with new emergent properties. A good example is Newton’s laws of motion and universal gravitation. Like the simple rules of Conway’s Game of Life give rise to complex patterns and gliders, the Newtonian equations lie at the core of some physical phenomena that were probably unimagined at the time of their conception. Rockets and gravitational slingshots to name a few.  Statistical Mechanics is also replete with the examples of emergent properties of matter. The macroscopic properties of matter like temperature and pressure, both are emergent. More recently, with the rapid development of the information technology, we have seen several decentralized systems emerge like the internet and cryptocurrencies. 

Modern science is still trying to come up with answers to some of the most pressing questions of our times. These include I) Abiogenesis – the emergence of life from purely abiotic physical and chemical environments and II) the emergence of consciousness from our brains. To understand the nature of life and the universe, an understanding of emergent properties is necessary. As established in this essay, the behavior of the ‘whole’ is always more complex than the behavior of the individual parts. It is not unreasonable to assert that the actual gameplay is as fundamental as the rules are. Summing it up, everything that existence entails seems to be an invocation of emergence at some level of complexity.

Cite as

Bader, Shujaut H., “The game of life: An essay on the beauty of complexity, emergence, and life.” Backscatter, September 13, 2020, https://backscatterblog.blogspot.com/2020/09/the-game-of-life.html

References

1. https://en.wikipedia.org/wiki/Chess
2. https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life
3. Audio in the Game of Life Video 1: 'Requiem for a Dream' soundtrack from the 2000 film Requiem for a Dream. Composer Clint Mansell.
4. Audio in the Game of Life Video 2: 'Call Me Joker' soundtrack from the 2019 film Joker. Composer: Hildur Guðnadóttir.